Re: A Hypothetical
Posted: Wed Jul 31, 2013 3:56 pm
We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
Permanent Portfolio Forum
https://www.gyroscopicinvesting.com/forum/
https://www.gyroscopicinvesting.com/forum/viewtopic.php?t=4989
You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
If that was the case, I would be beating a path to my broker's door to buy 8 times as many 7.7% bonds as I could 15.21% bonds. Wouldn't everybody? I mean, stop to imagine that for a second. Is it really plausible that a bond yielding half as much would be selling for one eighth the price?MediumTex wrote:You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
Right now, the 30 year bond is yielding 3.64%. A $1,000 investment will pay $36.40 per year in coupon payments.Pointedstick wrote:If that was the case, I would be beating a path to my broker's door to buy 8 times as many 7.7% bonds as I could 15.21% bonds. Wouldn't everybody? I mean, stop to imagine that for a second. Is it really plausible that a bond yielding half as much would be selling for one eighth the price?MediumTex wrote:You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
Right, so your NET loss after holding your 30 year bond between 1977 and 1981 is about $108 because your $1,000 investment is now worth $512 and you have collected $385 along the way.Fragile Bill wrote: Yes, the present value of the $1000 itself (excluding the interest stream) in 30 years at 15.21% is $12.30.
$12.30 X ((1 + .1521/2) ^ 60) = $1000
Add in the PV of the interest stream, $38.50 twice a year for 30 years, and you get to $512.
Right. That's your price to purchase it, which is about half as much. Half as much interest = half as much purchase price.Fragile Bill wrote: Yes, the present value of the $1000 itself (excluding the interest stream) in 30 years at 15.21% is $12.30.
$12.30 X ((1 + .1521/2) ^ 60) = $1000
Add in the PV of the interest stream, $38.50 twice a year for 30 years, and you get to $512.
Here's a question for you:MangoMan wrote:MediumTex wrote:You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
If you are saying that the bonds would instead be selling for $512, then we're back to the original point that $512 is the price of the bond, and the interest payments over a period of time would need to be added to this value to determine what the actual net gain or loss was for the period the bond was held.
http://www.investopedia.com/calculator/ ... cdate.aspx
If I understand duration correctly, a duration of 12 means that a 1% rise in interest rates will cause the bond's principal value to decline by 12%. So a 7.5% change in rates would cause a 90% reduction in the value of the bond? That can't be right...
MT,MediumTex wrote:Here's a question for you:MangoMan wrote:MediumTex wrote: You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
If you are saying that the bonds would instead be selling for $512, then we're back to the original point that $512 is the price of the bond, and the interest payments over a period of time would need to be added to this value to determine what the actual net gain or loss was for the period the bond was held.
http://www.investopedia.com/calculator/ ... cdate.aspx
If I understand duration correctly, a duration of 12 means that a 1% rise in interest rates will cause the bond's principal value to decline by 12%. So a 7.5% change in rates would cause a 90% reduction in the value of the bond? That can't be right...
If a 30 year bond yielded 10%, cost $1,000, and paid you $100 per year, how much would you pay for a 30 year bond that paid you $50 per year? Would you pay $500 for it? If it had originally been issued at $1,000 back when interest rates were at 5%, wouldn't it be accurate to say that the intervening rise in interest rates from 5% to 10% had caused the 5% bond to lose precisely 50% of its value?
A one year bond situation is much easier to calculate because there is only one or maybe two payments to consider.moda0306 wrote: I'm sure you're not suggesting this, but if I have a 1 year bond paying me $50 per year when the equivalent bonds are now yielding $100, my bond isn't worth half as much as theirs... nowhere close in fact.
Ok so if my calculations are correct, a 30 year bond purchased today at 3.644% would lose around 4% per year (including reinvested interest) if rates double over the next 5 years. The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.MediumTex wrote: Let me try to say it more directly:
If I buy a 7.7% 30 year bond for $1,000 today and sell it five years from now for $512, I have a capital loss of $488.
However, during that five year period I collected $385 in dividends, which I would need to consider in thinking about my actual investment performance.
When I include my dividends, my $488 loss, looks more like a $103 loss, or about a 2% loss for each year during which I owned the bond.
Take a look at the 1977-1981 figures and you will see that this average annual 2% loss is about what occurred.
In real terms, of course, that 2% annual loss was much greater, but 2% was the loss each year in nominal terms.
The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
It might be no less bad from a price standpoint (near 50% loss) but you collect lower coupon payments.MediumTex wrote:The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
Yes, but when you introduce inflation into the picture, the effects are not as bad in real terms as it may at first appear.dragoncar wrote:It might be no less bad from a price standpoint (near 50% loss) but you collect lower coupon payments.MediumTex wrote:The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
It's just a very well worn path in many people's minds.Reub wrote: And why are we so certain rates are even going to rise?
http://gyroscopicinvesting.com/forum/bo ... recession/
http://gyroscopicinvesting.com/forum/bo ... t-reached/
I don't think we are. But what if rates fall? Well the higher rate environment still seems superior.Reub wrote: And why are we so certain rates are even going to rise?
http://gyroscopicinvesting.com/forum/bo ... recession/
http://gyroscopicinvesting.com/forum/bo ... t-reached/
I'm not sure if your calculations are right because that's not an easy task and I think most online bond calculators are wrong, but anyways your example is not fair. In the first one there is a full 500 basis points reduction in the yield, but in the second just 182bp or barely a third. Keep in mind that rate changes are not exponential, but progressive.dragoncar wrote: Edit example for 1000 par value:
10-5% results in $1645 plus $100 per year
3.644-1.822% results in $1316 plus $36 per year
That's news to me about calculators. Please share.brownehead wrote:I'm not sure if your calculations are right because that's not an easy task and I think most online bond calculators are wrong, but anyways your example is not fair. In the first one there is a full 500 basis points reduction in the yield, but in the second just 182bp or barely a third. Keep in mind that rate changes are not exponential, but progressive.dragoncar wrote: Edit example for 1000 par value:
10-5% results in $1645 plus $100 per year
3.644-1.822% results in $1316 plus $36 per year
For a precise calculation it should be used convexity calculation, which is a complex task and I'm not sure if every online bond calculator do that. Btw my own calcs for you example and a 30y bond are:dragoncar wrote:That's news to me about calculators. Please share.
I can imagine some extreme scenarios for long term bonds going to 0 yield and bellow (for exemple very long term deflation, cash bans and widespread bank failures), but that's not the point. The real point is that in the way from 3.67% rates to 0% would be gigantic bond price appreciation (due to the convexity property).dragoncar wrote: If rate changes are progressive, then I guess we do have a lot to fear about being so close to zero (since we can't go below zero in this -5 example)
With current yield at 3.644%, going to 2.644% you win 20.5% (in price appreciation) and going to 4.644% you lost 16%.dragoncar wrote: Edit: what would be a fair comparison in both upside and downside directions? Is it ok to compare 5-10 with 3.644-8.644?
Since I don't have a working calculator... What is the upside if rates go to 0? Also which calculator do you recommend? I think I used investopediabrownehead wrote:For a precise calculation it should be used convexity calculation, which is a complex task and I'm not sure if every online bond calculator do that. Btw my own calcs for you example and a 30y bond are:dragoncar wrote:That's news to me about calculators. Please share.
for 1000 par value:
10-5% results in $1768.65 price appreciation
3.644-1.822% results in $1418.2 price appreciation
I can imagine some extreme scenarios for long term bonds going to 0 yield and bellow (for exemple very long term deflation, cash bans and widespread bank failures), but that's not the point. The real point is that in the way from 3.67% rates to 0% would be gigantic bond price appreciation (due to the convexity property).dragoncar wrote: If rate changes are progressive, then I guess we do have a lot to fear about being so close to zero (since we can't go below zero in this -5 example)
With current yield at 3.644%, going to 2.644% you win 20.5% (in price appreciation) and going to 4.644% you lost 16%.dragoncar wrote: Edit: what would be a fair comparison in both upside and downside directions? Is it ok to compare 5-10 with 3.644-8.644?
With yield at 10%, going to 9% you win 10.3% and going to 11% you lost 9%.
In my view the downside direction has more potential for gains, and with low yields the associated highest volatily is perfect for the Permanent Portfolio (and you are talking with a man who own german bonds with 2.4% yields).
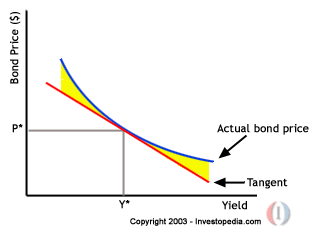
But brownehead's calculation above shows that bond prices are LESS sensitive to a halving of yields at lower interest rates, compared to a halving at higher interest rates.TennPaGa wrote:This is not the case; dragoncar is right. Bonds are more sensitive to yield changes the lower the yield.MediumTex wrote:The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
For a bond having face value F with N annual coupon payments at yield R (and a face value payment in year N), the bond price when the prevailing interest rate is r is:
P = sum(n = 1 to N, F*R/(1+r)^n) + F/(1+r)^N
The summation term is a geometric series, so the expression can be simplified to:
P = F * R/r * [1 - 1/(1+r)^N] + F/(1+r)^N
which can also be simplified to
P = F * [ R/r + (1 - R/r)/(1+r)^N ]
If what MT is saying were true, then price would only be a function of R/r. As you can see, it is not.
Or maybe you are saying the 100 basis points between 8% and 7% would cause less appreciation than a 100 basis point move between 4% and 3%, which is an important but simpler point.for 1000 par value:
10-5% results in $1768.65 price appreciation
3.644-1.822% results in $1418.2 price appreciation