A Hypothetical
Moderator: Global Moderator
-
Fragile Bill
- Associate Member

- Posts: 30
- Joined: Sun Jul 28, 2013 5:27 pm
Re: A Hypothetical
We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
Re: A Hypothetical
You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
If you are saying that the bonds would instead be selling for $512, then we're back to the original point that $512 is the price of the bond, and the interest payments over a period of time would need to be added to this value to determine what the actual net gain or loss was for the period the bond was held.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
- Pointedstick
- Executive Member

- Posts: 8883
- Joined: Tue Apr 17, 2012 9:21 pm
- Contact:
Re: A Hypothetical
If that was the case, I would be beating a path to my broker's door to buy 8 times as many 7.7% bonds as I could 15.21% bonds. Wouldn't everybody? I mean, stop to imagine that for a second. Is it really plausible that a bond yielding half as much would be selling for one eighth the price?MediumTex wrote:You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
Human behavior is economic behavior. The particulars may vary, but competition for limited resources remains a constant.
- CEO Nwabudike Morgan
- CEO Nwabudike Morgan
Re: A Hypothetical
Let me try to say it more directly:
If I buy a 7.7% 30 year bond for $1,000 today and sell it five years from now for $512, I have a capital loss of $488.
However, during that five year period I collected $385 in dividends, which I would need to consider in thinking about my actual investment performance.
When I include my dividends, my $488 loss, looks more like a $103 loss, or about a 2% loss for each year during which I owned the bond.
Take a look at the 1977-1981 figures and you will see that this average annual 2% loss is about what occurred.
In real terms, of course, that 2% annual loss was much greater, but 2% was the loss each year in nominal terms.
If I buy a 7.7% 30 year bond for $1,000 today and sell it five years from now for $512, I have a capital loss of $488.
However, during that five year period I collected $385 in dividends, which I would need to consider in thinking about my actual investment performance.
When I include my dividends, my $488 loss, looks more like a $103 loss, or about a 2% loss for each year during which I owned the bond.
Take a look at the 1977-1981 figures and you will see that this average annual 2% loss is about what occurred.
In real terms, of course, that 2% annual loss was much greater, but 2% was the loss each year in nominal terms.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
-
Fragile Bill
- Associate Member

- Posts: 30
- Joined: Sun Jul 28, 2013 5:27 pm
Re: A Hypothetical
Yes, the present value of the $1000 itself (excluding the interest stream) in 30 years at 15.21% is $12.30.
$12.30 X ((1 + .1521/2) ^ 60) = $1000
Add in the PV of the interest stream, $38.50 twice a year for 30 years, and you get to $512.
$12.30 X ((1 + .1521/2) ^ 60) = $1000
Add in the PV of the interest stream, $38.50 twice a year for 30 years, and you get to $512.
Re: A Hypothetical
Right now, the 30 year bond is yielding 3.64%. A $1,000 investment will pay $36.40 per year in coupon payments.Pointedstick wrote:If that was the case, I would be beating a path to my broker's door to buy 8 times as many 7.7% bonds as I could 15.21% bonds. Wouldn't everybody? I mean, stop to imagine that for a second. Is it really plausible that a bond yielding half as much would be selling for one eighth the price?MediumTex wrote:You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
A bond with a yield of 1.82% would cost $500 because that's what would make it comparable to a $1,000 investment yielding twice as much. Whatever interest either bond may have generated in the past is irrelevant to the way it is priced today based upon its future payment stream.
A 50% increase in interest rates should result in a 50% decline in a bond's value.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
Re: A Hypothetical
Right, so your NET loss after holding your 30 year bond between 1977 and 1981 is about $108 because your $1,000 investment is now worth $512 and you have collected $385 along the way.Fragile Bill wrote: Yes, the present value of the $1000 itself (excluding the interest stream) in 30 years at 15.21% is $12.30.
$12.30 X ((1 + .1521/2) ^ 60) = $1000
Add in the PV of the interest stream, $38.50 twice a year for 30 years, and you get to $512.
Do you disagree?
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
- Pointedstick
- Executive Member

- Posts: 8883
- Joined: Tue Apr 17, 2012 9:21 pm
- Contact:
Re: A Hypothetical
Right. That's your price to purchase it, which is about half as much. Half as much interest = half as much purchase price.Fragile Bill wrote: Yes, the present value of the $1000 itself (excluding the interest stream) in 30 years at 15.21% is $12.30.
$12.30 X ((1 + .1521/2) ^ 60) = $1000
Add in the PV of the interest stream, $38.50 twice a year for 30 years, and you get to $512.
The payments you receive are real money. You get real dollars. You have them in your hand. You get to add their value to the sale price you could receive if you sold the bond. You could sell your bond for $512 to someone else, but once you do that, you don't have to give them the payments you've already received! That's why $512 includes the PV of the interest for the future owner, but you--the holder of the bond today--get to add the interest payments you actually already received to the sale price when determining your gain or loss.
Put more simply and hypothetically, if you buy a bond for $1000, hold it for 5 years during which time it gives you $500, then sell it for $500, you broke even.
Human behavior is economic behavior. The particulars may vary, but competition for limited resources remains a constant.
- CEO Nwabudike Morgan
- CEO Nwabudike Morgan
Re: A Hypothetical
Here's a question for you:MangoMan wrote:MediumTex wrote:You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?Fragile Bill wrote: We're talking 30 year bonds. So the PV of a $1000 bond with a 7.70% coupon rate when the prevailing rate is 15.21% is $12.30. Add the PV of the interest stream and you get to $512.
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
If you are saying that the bonds would instead be selling for $512, then we're back to the original point that $512 is the price of the bond, and the interest payments over a period of time would need to be added to this value to determine what the actual net gain or loss was for the period the bond was held.
http://www.investopedia.com/calculator/ ... cdate.aspx
If I understand duration correctly, a duration of 12 means that a 1% rise in interest rates will cause the bond's principal value to decline by 12%. So a 7.5% change in rates would cause a 90% reduction in the value of the bond? That can't be right...
If a 30 year bond yielded 10%, cost $1,000, and paid you $100 per year, how much would you pay for a 30 year bond that paid you $50 per year? Would you pay $500 for it? If it had originally been issued at $1,000 back when interest rates were at 5%, wouldn't it be accurate to say that the intervening rise in interest rates from 5% to 10% had caused the 5% bond to lose precisely 50% of its value?
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
Re: A Hypothetical
MT,MediumTex wrote:Here's a question for you:MangoMan wrote:MediumTex wrote: You're saying that an interest rate move from 7.70% to 15.21% will cause a 7.7% bond to lose about 98.7% of its value?
I don't believe that. I don't think that when rates are 15.21% and 15.21% bonds are selling for $1,000, that 7.70% bonds would be selling for $12.30.
If you are saying that the bonds would instead be selling for $512, then we're back to the original point that $512 is the price of the bond, and the interest payments over a period of time would need to be added to this value to determine what the actual net gain or loss was for the period the bond was held.
http://www.investopedia.com/calculator/ ... cdate.aspx
If I understand duration correctly, a duration of 12 means that a 1% rise in interest rates will cause the bond's principal value to decline by 12%. So a 7.5% change in rates would cause a 90% reduction in the value of the bond? That can't be right...
If a 30 year bond yielded 10%, cost $1,000, and paid you $100 per year, how much would you pay for a 30 year bond that paid you $50 per year? Would you pay $500 for it? If it had originally been issued at $1,000 back when interest rates were at 5%, wouldn't it be accurate to say that the intervening rise in interest rates from 5% to 10% had caused the 5% bond to lose precisely 50% of its value?
It depends on what Principal needs to be paid back on the $50 vs $100, and when it's going to be paid back.
I'm sure you're not suggesting this, but if I have a 1 year bond paying me $50 per year when the equivalent bonds are now yielding $100, my bond isn't worth half as much as theirs... nowhere close in fact.
However, you guys are right... you HAVE to count income for there to be any relevance at all. Especially when you're dealing with bonds, whose main draw is the income they pay you, not price changes. With stocks, dividends are less important, but still vital if you want an accurate analysis.
Learning how to use a financial calculator is one of the best things I've ever learned. Most things besides my gold and other very defensive investments are usually best analyzed from a standpoint of cash-flows, risk, and opportunity cost. I've found it unlocks so many mysteries of finance with that simple tool.
For instance, when buying a new air-conditioner, I was presented two options... one gave me an energy credit and was projected to save me a certain amount every month for the life of the air conditioner. So, I had to figure out the variables first:
PV: (difference in price of Air Conditioners... constant)
N: (number of years the A/C should last... variable... somewhere between 15 and 40 years (my previous a/c unit was from 1975 haha))
PMT: (difference in utility bill... predictably constant today, but variable over time if energy prices or the price level in general rise rapidly)
FV: 0 (dead air conditioner)
%: (Solving for ROR)
So if you run the best-case and worst case scenarios within reason, you can get an idea of what your likely rates of return might be. But also have to remember that this is on an illiquid asset, so it's not like you can turn this into cash right away.
It was obvious that unless this thing ran for a LONG time and energy prices went up significantly, the rate of return of the more expensive a/c just wasn't worth it given what I think I could get and with more certainty out of a diversified, liquid portfolio.
You can do this with almost anything, big or small. Sometimes it's more complex and cash flows might be variable, but overall I almost think we could solve the problems in the middle east with a financial calculator if we could figure out how to apply the variables correctly.
"Men did not make the earth. It is the value of the improvements only, and not the earth itself, that is individual property. Every proprietor owes to the community a ground rent for the land which he holds."
- Thomas Paine
- Thomas Paine
Re: A Hypothetical
A one year bond situation is much easier to calculate because there is only one or maybe two payments to consider.moda0306 wrote: I'm sure you're not suggesting this, but if I have a 1 year bond paying me $50 per year when the equivalent bonds are now yielding $100, my bond isn't worth half as much as theirs... nowhere close in fact.
Let's say that I pay $1,000 today to receive $1,050 back in one year because ST rates are 5%. In other words, the bond is paying me $50 in interest.
If, however, short term rates suddenly shoot up to 10%, the question would be how much my 5% one year bond was now worth.
Well, we know my bond will pay $1,050 in one year, and we know that investors now expect to get a 10% return on their one year bond investments. Thus, in order for my $1,050 bond to provide a 10% return, an investor would only be willing to pay about $955 for it (i.e., investor pays $955 and gets back $955+10% in one year, which is about $1,050).
Thus, an interest rate move from 5% to 10% would cause a 4.5% reduction in the value of my one year bond (I bought it for $1,000, but could only sell it for $955 when interest rates increased).
These moves are, of course, amplified as you move further out on the yield curve.
Do you agree?
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
Re: A Hypothetical
Ok so if my calculations are correct, a 30 year bond purchased today at 3.644% would lose around 4% per year (including reinvested interest) if rates double over the next 5 years. The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.MediumTex wrote: Let me try to say it more directly:
If I buy a 7.7% 30 year bond for $1,000 today and sell it five years from now for $512, I have a capital loss of $488.
However, during that five year period I collected $385 in dividends, which I would need to consider in thinking about my actual investment performance.
When I include my dividends, my $488 loss, looks more like a $103 loss, or about a 2% loss for each year during which I owned the bond.
Take a look at the 1977-1981 figures and you will see that this average annual 2% loss is about what occurred.
In real terms, of course, that 2% annual loss was much greater, but 2% was the loss each year in nominal terms.
Re: A Hypothetical
The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
Re: A Hypothetical
It might be no less bad from a price standpoint (near 50% loss) but you collect lower coupon payments.MediumTex wrote:The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
Re: A Hypothetical
Yes, but when you introduce inflation into the picture, the effects are not as bad in real terms as it may at first appear.dragoncar wrote:It might be no less bad from a price standpoint (near 50% loss) but you collect lower coupon payments.MediumTex wrote:The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
Re: A Hypothetical
And why are we so certain rates are even going to rise?
http://gyroscopicinvesting.com/forum/bo ... recession/
http://gyroscopicinvesting.com/forum/bo ... t-reached/
http://gyroscopicinvesting.com/forum/bo ... recession/
http://gyroscopicinvesting.com/forum/bo ... t-reached/
Re: A Hypothetical
It's just a very well worn path in many people's minds.Reub wrote: And why are we so certain rates are even going to rise?
http://gyroscopicinvesting.com/forum/bo ... recession/
http://gyroscopicinvesting.com/forum/bo ... t-reached/
It just seems like something that should happen.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”
Re: A Hypothetical
I don't think we are. But what if rates fall? Well the higher rate environment still seems superior.Reub wrote: And why are we so certain rates are even going to rise?
http://gyroscopicinvesting.com/forum/bo ... recession/
http://gyroscopicinvesting.com/forum/bo ... t-reached/
As to MT's point re inflation, I'm not sure if its just a general sense that inflation is worse in higher rate environments or if there is some mathematical relationship between inflation and rates that we can use to compare total real bond returns for different yield changes.
Edit example for 1000 par value:warning these numbers appear to have been debunked later in the thread
10-5% results in $1645 plus $100 per year
3.644-1.822% results in $1316 plus $36 per year
Last edited by dragoncar on Thu Aug 01, 2013 2:40 pm, edited 1 time in total.
-
brownehead
- Associate Member

- Posts: 36
- Joined: Thu Apr 18, 2013 5:59 pm
- Location: Spain
- Contact:
Re: A Hypothetical
I'm not sure if your calculations are right because that's not an easy task and I think most online bond calculators are wrong, but anyways your example is not fair. In the first one there is a full 500 basis points reduction in the yield, but in the second just 182bp or barely a third. Keep in mind that rate changes are not exponential, but progressive.dragoncar wrote: Edit example for 1000 par value:
10-5% results in $1645 plus $100 per year
3.644-1.822% results in $1316 plus $36 per year
Cartera Permanente para un mundo incerto
Re: A Hypothetical
That's news to me about calculators. Please share.brownehead wrote:I'm not sure if your calculations are right because that's not an easy task and I think most online bond calculators are wrong, but anyways your example is not fair. In the first one there is a full 500 basis points reduction in the yield, but in the second just 182bp or barely a third. Keep in mind that rate changes are not exponential, but progressive.dragoncar wrote: Edit example for 1000 par value:
10-5% results in $1645 plus $100 per year
3.644-1.822% results in $1316 plus $36 per year
If rate changes are progressive, then I guess we do have a lot to fear about being so close to zero (since we can't go below zero in this -5 example)
Edit: what would be a fair comparison in both upside and downside directions? Is it ok to compare 5-10 with 3.644-8.644?
Last edited by dragoncar on Thu Aug 01, 2013 5:40 am, edited 1 time in total.
-
brownehead
- Associate Member

- Posts: 36
- Joined: Thu Apr 18, 2013 5:59 pm
- Location: Spain
- Contact:
Re: A Hypothetical
For a precise calculation it should be used convexity calculation, which is a complex task and I'm not sure if every online bond calculator do that. Btw my own calcs for you example and a 30y bond are:dragoncar wrote:That's news to me about calculators. Please share.
for 1000 par value:
10-5% results in $1768.65 price appreciation
3.644-1.822% results in $1418.2 price appreciation
I can imagine some extreme scenarios for long term bonds going to 0 yield and bellow (for exemple very long term deflation, cash bans and widespread bank failures), but that's not the point. The real point is that in the way from 3.67% rates to 0% would be gigantic bond price appreciation (due to the convexity property).dragoncar wrote: If rate changes are progressive, then I guess we do have a lot to fear about being so close to zero (since we can't go below zero in this -5 example)
With current yield at 3.644%, going to 2.644% you win 20.5% (in price appreciation) and going to 4.644% you lost 16%.dragoncar wrote: Edit: what would be a fair comparison in both upside and downside directions? Is it ok to compare 5-10 with 3.644-8.644?
With yield at 10%, going to 9% you win 10.3% and going to 11% you lost 9%.
In my view the downside direction has more potential for gains, and with low yields the associated highest volatily is perfect for the Permanent Portfolio (and you are talking with a man who own german bonds with 2.4% yields).
Cartera Permanente para un mundo incerto
Re: A Hypothetical
Since I don't have a working calculator... What is the upside if rates go to 0? Also which calculator do you recommend? I think I used investopediabrownehead wrote:For a precise calculation it should be used convexity calculation, which is a complex task and I'm not sure if every online bond calculator do that. Btw my own calcs for you example and a 30y bond are:dragoncar wrote:That's news to me about calculators. Please share.
for 1000 par value:
10-5% results in $1768.65 price appreciation
3.644-1.822% results in $1418.2 price appreciation
I can imagine some extreme scenarios for long term bonds going to 0 yield and bellow (for exemple very long term deflation, cash bans and widespread bank failures), but that's not the point. The real point is that in the way from 3.67% rates to 0% would be gigantic bond price appreciation (due to the convexity property).dragoncar wrote: If rate changes are progressive, then I guess we do have a lot to fear about being so close to zero (since we can't go below zero in this -5 example)
With current yield at 3.644%, going to 2.644% you win 20.5% (in price appreciation) and going to 4.644% you lost 16%.dragoncar wrote: Edit: what would be a fair comparison in both upside and downside directions? Is it ok to compare 5-10 with 3.644-8.644?
With yield at 10%, going to 9% you win 10.3% and going to 11% you lost 9%.
In my view the downside direction has more potential for gains, and with low yields the associated highest volatily is perfect for the Permanent Portfolio (and you are talking with a man who own german bonds with 2.4% yields).
-
brownehead
- Associate Member

- Posts: 36
- Joined: Thu Apr 18, 2013 5:59 pm
- Location: Spain
- Contact:
Re: A Hypothetical
Sorry but I'm not sure about any calculator when we use very low yields. But you can have an idea about the upside potential for price appreciation with a typical convexity graph:
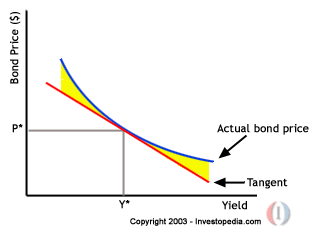

Cartera Permanente para un mundo incerto
Re: A Hypothetical
But brownehead's calculation above shows that bond prices are LESS sensitive to a halving of yields at lower interest rates, compared to a halving at higher interest rates.TennPaGa wrote:This is not the case; dragoncar is right. Bonds are more sensitive to yield changes the lower the yield.MediumTex wrote:The convexity of the yield curve and the way it affects bond pricing should make the point you start on the yield curve irrelevant.dragoncar wrote: The fact that we are currently in very low yield territory makes a rate doubling hurt a lot more.
The move from 2%-4% should be no more or less bad than a move from 4%-8%.
Maybe someone will do the math to show why this is the case.
For a bond having face value F with N annual coupon payments at yield R (and a face value payment in year N), the bond price when the prevailing interest rate is r is:
P = sum(n = 1 to N, F*R/(1+r)^n) + F/(1+r)^N
The summation term is a geometric series, so the expression can be simplified to:
P = F * R/r * [1 - 1/(1+r)^N] + F/(1+r)^N
which can also be simplified to
P = F * [ R/r + (1 - R/r)/(1+r)^N ]
If what MT is saying were true, then price would only be a function of R/r. As you can see, it is not.
Or maybe you are saying the 100 basis points between 8% and 7% would cause less appreciation than a 100 basis point move between 4% and 3%, which is an important but simpler point.for 1000 par value:
10-5% results in $1768.65 price appreciation
3.644-1.822% results in $1418.2 price appreciation
I agree that there is not an exact correlation between yield halving and doubling at different points on the yield curve for 30 year bonds, but the point I am generally making in these discussions is that there is a heck of a lot more potential price appreciation at very low yields than people often imagine.
As a practical matter, your PP can do very well if 30 year bond yields bounce between the mid-2% and low 4% range, and many people don't seem aware of how much money can be made in this kind of situation.
Thanks to all for clarifying these bond pricing scenarios.
Q: “Do you have funny shaped balloons?”
A: “Not unless round is funny.”
A: “Not unless round is funny.”